ВАРИАНТЫ ЗАДАНИЙ КОНТРОЛЬНОЙ РАБОТЫ N1

        Задание на контрольную работу включает выполнение трех задач для варианта исходных данных, приведенного в таблице 1:

        1) представить десятичное число N в виде двухбайтового шестнадцатеричного и двухбайтового двоичного числа; записать дополнительный код числа минус N;

        2) спроектировать сигнальное устройство, светодиод на выходе которого горит в том случае, если сработало N1 из N2 контактных датчиков;

        3) спроектировать синхронный счетчик, реализующий заданную последовательность смены состояний.

Таблица 1
Номер варианта N N1 N2 Состояния счетчика
1 265 3 14 6 5 7 3 2 1 0
2 273 4 13 7 6 5 0 3 2 1
3 517 3 13 0 2 3 4 1 6 5
4 529 4 14 0 1 3 5 7 6 4
5 285 5 12 0 4 5 7 2 3
6 297 3 11 0 2 3 5 7 4
7 548 4 10 1 6 4 7 2 5
8 1035 6 10 0 4 2 5 3 6
9 1043 3 8 0 5 7 4 6 1 3
10 1059 4 8 0 1 4 2 5 3 7
11 1086 5 8 0 3 2 1 4 7 6
12 1344 6 8 0 3 5 2 4 7 6
13 1857 4 9 2 4 6 1 7 0 5
14 2058 5 9 0 1 5 2 6 4 7
15 2066 6 9 4 2 7 0 1 6 3
16 2077 8 9 5 4 3 6 2 0 1
17 2139 3 9 6 4 2 7 3 1 0
18 2177 2 9 7 2 4 3 6 1 0
19 2433 3 10 0 5 2 6 3 1
20 2947 4 10 6 1 4 7 2 5 0
21 3968 5 10 7 0 5 4 3 6 1
22 4107 6 10 0 1 3 4 7 6 5
23 4115 7 10 6 1 3 5 7 0 4
24 4129 8 10 7 4 5 6 2 3
25 4157 5 11 0 2 3 5 6 4
26 4226 6 11 1 6 4 0 2 5
27 4352 7 11 0 7 2 5 3 6
28 4609 8 11 0 7 1 4 6 2 3
29 5634 9 11 1 4 2 0 5 3 6
30 5637 10 11 0 3 2 5 4 7 6
31 5657 4 11 1 0 5 2 4 7 6
32 5687 3 11 2 4 6 1 7 0 5
33 5815 7 12 3 0 5 2 6 4 7
34 5943 10 12 4 6 7 0 1 5 3
35 773 11 12 5 7 4 6 2 0 1
36 3459 5 12 7 1 5 3 2 4 6
37 999 6 12 9 8 7 6 5 3 2 1 0
38 1667 8 12 0 2 3 5 7 6 4 1 8
39 2777 9 12 0 3 5 7 2 4 6 8 9
40 3899 4 12 0 1 3 4 6 2 7 5 9

ПРИМЕР ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ N1

        Задание: N=799, N1=5, N2=9. Последовательность смены состояний счетчика: 5, 4, 3, 2, 1, 0 (т.е. необходимо спроектировать вычитающий двоичный счетчик с коэффициентом пересчета Ксч = 6).

        Задача 1.

        Записав остатки от деления 799 на 16, получаем шестнадцатеричный код числа 031FH. Представив каждую цифру шестнадцатеричного числа в виде четырехразрядного двоичного, получаем двоичный код числа 0000001100011111В. Инвертируя код числа N и добавляя единицу, получаем дополнительный код числа минус N (1111110011100001B или 0FCE1H).

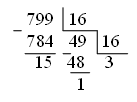
        дополнительный код N - 031F Н

        его инверсия - FCE0Н

        дополнительный код -N - FCE1Н

        Задача 2.

        Спроектируем сигнальное устройство, зажигающее светодиод, если сработали любые 5 из 9 датчиков. Одни клеммы контактов всех датчиков заземлим, а другие через резисторы сопротивлением 1 кОм подключим к источнику питания плюс 5В и подадим на входы устройства 1-9. Просуммируем число сработавших датчиков с помощью сумматоров (рис.1).

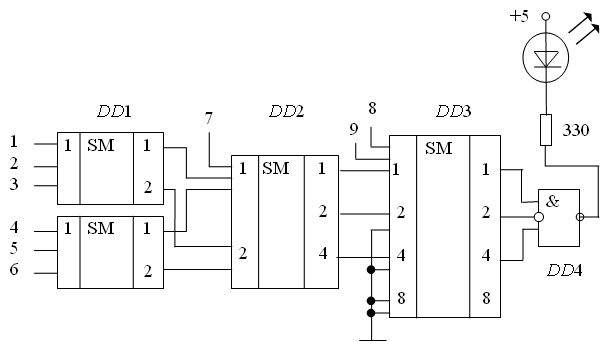
Рисунок 1 - Сигнальное устройство

        Логический элемент на выходе устройства формирует логический ноль, необходимый для того, чтобы горел светодиод, только при суммарном количестве сработавших датчиков, равном пяти. В устройстве можно задействовать микросхемы К555ИМ1 (DD1), К555ИМ2 (DD2), К555ИМ3 (DD3), К555ЛА4 (DD4). Резистор задает рабочий ток светодиода порядка 10 мА.

        Задача 3.

        Стоит задача спроектировать вычитающий двоичный счетчик с коэффициентом пересчета Ксч = 6. Для фиксации шести состояний счетчика возьмем три тактируемых по положительному фронту D-триггера, объединенные входы синхронизации которых будем использовать как счетный вход счетчика (рис. 2). Будем характеризовать состояние счетчика N трехразрядным двоичным словом Q3Q2Q1 (N должно циклически меняться от 5 до 0).

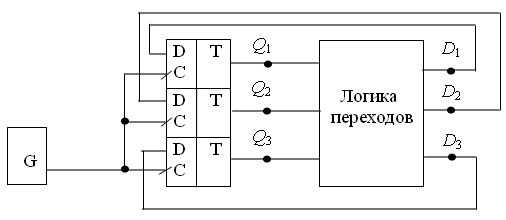
Рисунок 2 - Функциональная схема счетчика

        Каждый импульс генератора G переписывает на выходы триггеров Q3, Q2, Q1 информацию с входов D1, D2, D3. Поэтому дальнейший синтез счетчика сводится к построению комбинационной схемы (логики переходов), формирующей из выходных сигналов Q уровни сигналов D на информационных входах триггеров, необходимые для перехода в следующее состояние. Для этого составим таблицу переходов (табл. 2) и запишем логические выражения для сигналов D1, D2, D3 в ДНФ (дизъюнктивной нормальной форме):

         D 1 = Q 3 ⋅ Q 2 ¯ ⋅ Q 1 ¯ + Q 3 ¯ ⋅ Q 2 ⋅ Q 1 ¯ + Q 3 ¯ ⋅ Q 2 ¯ ⋅ Q 1 ¯ ; (1)
         D 2 = Q 3 ⋅ Q 2 ¯ ⋅ Q 1 ¯ + Q 3 ¯ ⋅ Q 2 ⋅ Q 1 ; (2)
         D 3 = Q 3 ⋅ Q 2 ¯ ⋅ Q 1 + Q 3 ¯ ⋅ Q 2 ¯ ⋅ Q 1 ¯ . (3)

        Для минимизации логических функций можно воспользоваться основными законами булевой алгебры или картами Карно (рис. 3), причем в клетках, соответствующих шестому и седьмому состоянию счетчика, логические функции можно доопределять по собственному усмотрению, так как в схеме проектируемого счетчика они не реализуются.

        По картам Карно запишем минимизированные выражения для функций D1 и D2

         D 1 = Q 1 ¯ ; (4)
         D 2 = Q 3 ⋅ Q 1 ¯ + Q 2 ⋅ Q 1 = Q 1 ⋅ Q 2 ¯ ⋅ Q 3 ⋅ Q 1 ¯ ¯ ¯ . (5)

        Выражение для D3 получим путем преобразования соотношения (3), так как карта Карно не позволяет провести эффективную минимизацию этой функции

         D 3 = Q 2 ¯ ( Q 3 ⋅ Q 1 + Q 3 ¯ ⋅ Q 1 ¯ )= Q 2 ¯ ⋅ Q 1 ⊕ Q 3 ¯ = Q 2 +( Q 1 ⊕ Q 3 ) ¯ . (6)
Таблица 2
Текущее состояние счетчика N Последующее состояние счетчика N+
N Q3 Q2 Q1 N+ D3 D2 D1
5 1 0 1 4 1 0 0
4 1 0 0 3 0 1 1
3 0 1 1 2 0 1 0
2 0 1 0 1 0 0 1
1 0 0 1 0 0 0 0
0 0 0 0 5 1 0 1

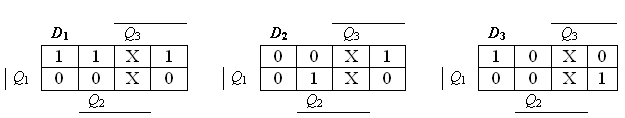
Рисунок 3 - Карты Карно для функций D1, D2, D3

        С учетом соотношений (4), (5) и (6) реализуем логику переходов на логических элементах (рис. 4). Ориентируясь на серию КР1533, выбираем для реализации устройства микросхемы триггеров КР1533ТМ2, логический элемент 2И-НЕ КР1533ЛА3, логический элемент 2ИЛИ-НЕ КР1533ЛЕ1, логический элемент "Исключающее ИЛИ" КР1533ЛП5. Инвертор реализуем путем объединения входов логического элемента 2И-НЕ.

        В отчет о выполнении контрольной работы рекомендуем включить файл проведения эксперимента по моделированию спроектированного устройства по методике выполнения лабораторных работ.

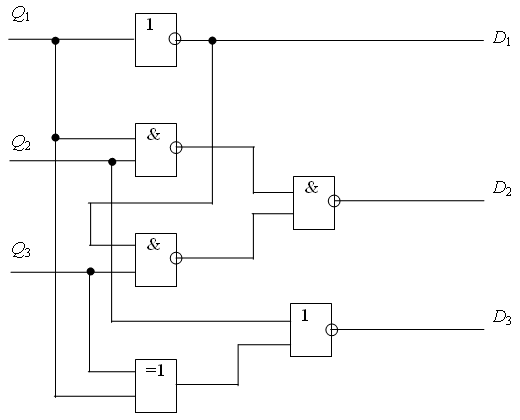
Рисунок 4 - Логика переходов