1.1. Системы счисленияСистема счисления - это совокупность приемов представления для обозначения натуральных чисел.Различают позиционные и непозиционные системы счисления. В позиционной системе счисления одна и та же цифра имеет различные значения в зависимости от места расположения. При этом предполагается, что имеется некоторое число n, если в первом разряде имеется ровно n единиц, то образуется единица во втором разряде, если имеется n единиц во втором разряде, то прибавляется единица в третий разряд и т.д.Такое число n называется основанием системы счислени. Основанием может быть любое натуральное число больше единицы.Итак, для того, чтобы задать позиционную систему счисления необходимо задать основание и алфавит, для изображения цифр. В десятичной системе счисления основанием является 10, а алфавит состоит из цифр {0,1,2,3,4,5,6,7,8,9}. В двоичной системе счисления основанием является 2, а алфавит - цифры {0,1}. В восьмеричной системе счисления основание равно 8, а алфавит состоит из следующих цифр (0,1,2,3,4,5,6,7). В шестнадцатеричной системе счисления основание равно 16, а алфавит состоит из цифр и букв (0,1,2,3,4,5,6,7,8,9,A,B,C,D,E). Например, 19610 (индекс означает основание системы счисления), или 100010112 , или 7128 , или A8F016. Можно представить любое число cnc
n-1 ...c1c0 в виде суммы некоторого ряда: ,где n -номер разряда числа; сj - цифра j-го разряда; o - основание. Тогда число 19610 можно записать следующим образом: а число 100010112 можно записать: число 7128 можно записать: a число A8F016 можно записать: Рассмотрим алгоритмы преобразования чисел из одной системы счисления в другую. Алгоритм преобразования числа cnc n-1 ...c1c0 в десятичную довольно прост и основан на использовании формулы (9.1). Необходимо отметить, что если вместо цифры в числе стоит буква, то ставится ее порядковый номер, например в числе A8F016 вместо A ставится 10, а вместо F ставится 15, тогда можно вычислить десятичный аналог числа A8F016 : Алгоритм преобразование десятичного числа D в другую систему счисления основан также на формуле (9.1), но более сложен. Предположим что D = cnon+cn-1on-1+...+c1o1+c0o0 , при этом основание o нам известно, необходимо найти соответствующие цифры cncn-1...c1c0. Тогда алгоритм будет следующий: Делим число D на основание, получим частное и остаток. Запоминаем остаток как c0, а частное cn on-1 + cn-1on-2+...+c1 делим снова на основание. Остаток от деления напишем как c1 , а частное cn on-2+ cn-1on-3+...+c2 . Далее находим остаток от делени c2 .Это процесс продолжается до тех пор, пока не получим cn и частное не станет равное нулю. Рассмотрим пример: Перевести десятичное число 43248 в шестнадцатеричное. 
Считая, что 15 - это E , а 10 - это A , то получим число A8F016 . Для перевода чисел из десятичной системы в двоичную используют этот же алгоритм, только применяют упрощенный вариант. Число раскладывают суммой степеней двойки. Например, число 525 можно представить суммой (512+8 +4 +1), соответственно (29+23+22+20 ), тогда двоичное число будет иметь единички только в разрядах с номерами 9, 3, 2 , 0, а само число 100001101. Для перевода в двоичную систему необходимо помнить значения степеней двойки. 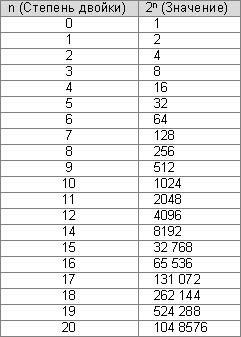
Перевод систем счисления с основанием,
кратным 2, довольно прост. Если необходимо перевести шестнадцатиразрядное число
в двоичное, то поступают следующим образом: каждый разряд шестнадцатеричного
числа представляют четырехразрядным двоичным числом, в соответствии с таблицей
1.2: 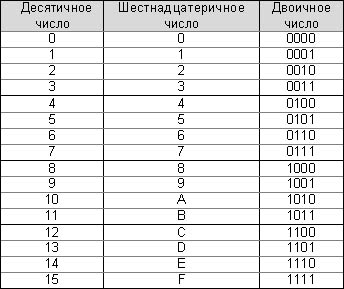
Преобразование двоичных чисел в
шестнадцатеричные также возможно, используя эту же таблицу, объединяя четыре
разряда в один разряд шестнадцатеричного числа. Например, двоичное число
10010111 преобразуется в шестнадцатеричное число: 0111 -7 ,1001 -B, тогда само
число - B 7 . Для восьмеричных чисел возможно построить такую же таблицу,
учитывая,что один разряд восьмеричного числа может быть представлен
трехразрядным двоичным числом. |