1.4. АлгоритмыСлово «алгоритм» произошло от арабского слова «Аль-Хорезми», имени среднеазиатского ученого, жившего в первом тысячелетии (приблизительно 825 г) в городе Хива (ныне Узбекистан) и написавшего книгу «Правила восстановления и преобразования». Когда говорят:"Алгоритм решения задачи",то подразумевают описание последовательности действий, приводящих к решению задачи.Толкование задачи может быть в самом широком смысле, например, приготовление пищи, открытие дверей, лечение больных кошек и т. д. Важный вопрос: "Всякое ли описание последовательности действий есть алгоритм?" Например, описание хаотического движения атомов не является алгоритмом. Для алгоритма присуще:
Для алгоритма характерно, чтобы решение задачи можно разбить на некоторую совокупность шагов, причем после выполнения очередного шага алгоритма всегда известен шаг, который будет следующим. Это свойство алгоритма называется «определенность» или «детерминированность». Другое свойство заключается в том, что последовательность шагов должна быть конечной, т. е. результат должен быть получен за конечное число шагов. Это свойство называется «конечность». И третье, основное свойство - «массовость», которое означает, что последовательность шагов может быть выполнена для решения некоторого класса задач. Итак, под алгоритмом понимается описание детерминированного процесса преобразования исходных данных в искомый результат. Основные свойства алгоритма:
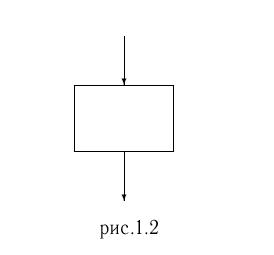
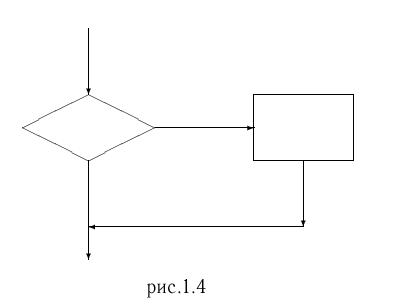
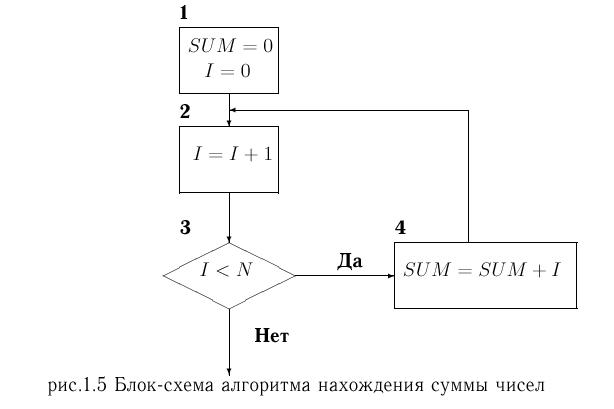
1.4.1. Способы записи алгоритмовСуществует достаточно большое разнообразие описания алгоритмов.Самый простой способ - это использовать обычный естественный язык. Например, алгоритм решения квадратного уравнения:
Такое описание алгоритма дает преимущества на самых первых шагах разработки алгоритма. Одно из обстоятельств, необходимых для использования этого способа - формулировка и фиксация основных моментов и идей разрабатываемого алгоритма. Идея, написанная на бумаге, может существенно отличаться от той, которая была в уме!!! |