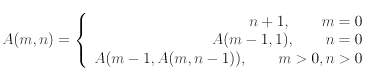.: [предыдущая | оглавление | следующая] :.

5.5 Функция Аккермана

Еще один наглядный пример простого алгоритма, но показывающего экспоненциальный взрыв времени вычисления. Функци Аккермана относитс к классу дважды рекурсивных и имеет следующий вид:

Ниже приведена рекурсивная функци подсчета.

int Akk(int m,int n)
{ //реализация подсчета функции Аккермана
      if(m==0) return n+1;
      if(n==0) return Akk(m-1,1);
      return Akk(m-1,Akk(m,n-1));
}

Теперь необходимо вычислить Akk(4,2)=?...попробуйте поэкспериментировать!

Запишем вно функцию Аккермана для фиксированных значений m (здесь приведены итоговые формулы, те кто хочет проверить, может сделать это сам, использу метод математической индукции и формулу геометрической прогрессии).

  1. A(0,n)=n+1, при m=0
  2. A(1,n)=n+2, при m=1
  3. A(2,n)=2*n+3, при m=2
  4. A(3,n)=(2^n+3) - 3, при m=3
Теперь запишем выражение для A(4,2):
        A(4,2)=A (3,A (4,1))=(2^A(4,1)+3)-3
        A(4,1)=A (3,A (4,0))=(2^A(4,0)+3)-3
        A(4,0)=A (3,1) = (2^1+3) - 3=16 - 3=13
        A(4,1)=(2^13+3) - 3 = 65536 - 3 =65533
        A(4,2)=(2^65533+3)-3

Вот итоговый факт, для представлени результирующего числа необходимо 65 килобит. Соответственно для подсчета такого числа необходимо 2^65533+3 вызовов функции Akk! Вот это и есть экспоненциальный взрыв!
.: [предыдущая | оглавление | следующая] :.