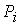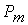Мера количества информации
Направления оценки количества информации
В теории информации выделяются три основных направления: структурное, статистическое, семантическое.
Структурное - рассматривает дискретное строение массивов информации и их измерение простым подсчетом информационных элементов. (Простейшее кодирование массивов - комбинаторный метод.)
Статистическое направление оперирует понятием энтропии как меры неопределенности, то есть здесь учитывается вероятность появления тех или иных сообщений.
Семантическое направление учитывает целесообразность, ценность или существенность информации.
Эти три направления имеют свои определенные области применения. Структурное используется для оценки возможностей технических средств различных систем переработки информации, независимо от конкретных условий их применения. Статистические оценки применяются при рассмотрении вопросов передачи данных, определении пропускной способности каналов связи. Семантические используются при решении задач построения систем передачи информации разработки кодирующих устройств и при оценке эффективности различных устройств.
Структурные меры информации
Структурные меры учитывают только дискретное строение информации. Элементами информационного комплекса являются кванты - неделимые части информации. Различают геометрическую, комбинаторную и аддитивную меры.
Определение информации геометрическим методом представляет собой измерение длины линии, площади или объема геометрической модели информационного комплекса в количестве квантов. Максимально возможное число квантов в заданных структурных габаритах определяет информационную емкость системы. Информационная емкость есть число, указывающее количество квантов в полном массиве информации. Согласно рис. 1.2, г, количество информации М в комплексе X(T,N), определенное геометрическим методом, равняется
М= 
,
где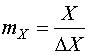 
; 
; 
;
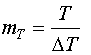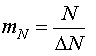Х, Т, N - интервалы, через которые осуществляются дискретные отсчеты.
В комбинаторной мере количество информации вычисляется как количество комбинаций элементов. Здесь учитываются возможные или реализованные комбинации.
Во многих случаях дискретное сообщение можно рассматривать как слово, состоящее из некоторого количества элементов n, заданных алфавитом, состоящим из т элементов-букв. Определим количество различных сообщений, которые можно образовать из данного алфавита. Если сообщение состоит из двух элементов (п=2), то всего может быть 
различных сообщений. Например, из десяти цифр (0, 1, 2,..., 9) может быть образовано сто различных чисел от 0 до 99. Если количество элементов равно трем, то количество различных сообщений равно 
и т.д.
Таким образом, число возможных сообщений определяется:
L= 
,
где L - число сообщений; п - число элементов в слове; т - алфавит.
Чем больше L, тем сильнее может отличаться каждое сообщение от остальных. Величина L может быть принята в качестве меры количества информации. Однако выбор L в качестве меры количества информации связан с неудобствами: во-первых, при L =1 информация равна нулю, поскольку заранее известен характер сообщения (т.е. сообщение есть, а информация равна нулю); во-вторых, не выполняется условие линейного сложения количества информации, т.е. условие аддитивности. Если, например, первый источник характеризуется 
различными сообщениями, а второй - 
, то общее число различных сообщений для двух источников определяется произведением
L= 
.
Для k источников общее число возможных различных сообщений равно
L= 
.
Поэтому Хартли ввел логарифмическую (аддитивную) меру количества информации, позволяющую оценивать количество инфомации, содержащейся в сообщении, логарифмом числа возможных сообщений.
I= 
.
Тогда при L=1 I=0, т.е. информация отсутствует.
Для k источников информации
I= 
,
т.е. I= 
.
Статистические меры информации
При статическом вероятностном подходе получение конкретного количества информации рассматривается как результат определенного выбора среди возможных сообщений. Получатель информации может заранее знать или угадать ее часть. Когда приходит сообщение о часто происходящих событиях, вероятность появления которых Р стремится к единице, то такое сообщение малоинформативно. Столь же малоинформативны в среднем сообщения о событиях, вероятности которых стремятся к нулю, т.е. о почти невозможных событиях, поскольку сообщения о таких событиях поступают чрезвычайно редко.
События можно рассматривать как возможные исходы некоторого опыта. Все исходы составляют полную группу событий, или ансамбль.
Ансамбль характеризуется тем, что сумма вероятностей всех сообщений в нем равна единице, то есть
.
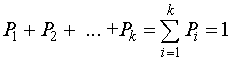Рассмотрим сложные сообщения, составляемые из п элементов, каждый из которых является независимым и выбирается из алфавита, содержащего т букв, с вероятностями выбора элементов 
соответственно. Предположим, что в некоторое сообщение вошло 
элементов 
алфавита, 
элементов 
и т.д. Такое сообщение характеризуется таблицей (табл. 1.1).
Таблица 1.1
| Тип элемента |  |
 |
 |
... |  |
... |  |
| Число элементов |  |
 |
 |
... |  |
... |  |
|
Вероятности выбора элементов |
|
|
|
... |
|
... |
|
Вероятность того, что в сообщение войдут 
элементов 
равняется 
, а вероятность образования сообщения из 
,
, 
,...,
,...,
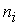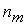элементов будет равна
Р= 
. (1.1)
При большой длине п источником будут формироваться типичные сообщения, в которых относительная частота появления отдельных элементов 
стремится к вероятности появления этих элементов, то есть
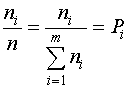, (1.2)
а вероятности появления типичных сообщений Р будут одинаковы и могут быть найдены из (1.1), (1.2):
Р=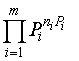 
. (1.3)
Определим число типичных сообщений:
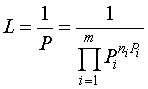, (1.4)
так как суммарная вероятность всех типичных сообщений стремится к единице при увеличении длины сообщений.
Хотя число возможных сообщений 
, источник практически будет вырабатывать только L типичных сообщений, а вероятность появления остальных сообщений стремится к нулю.
Найдем количество информации I, содержащейся в одном сообщении:
I= log L= -log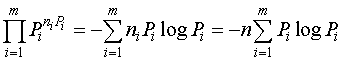
. (1.5)
Данное выражение (формула Шеннона) дает более полное представление об источнике информации, чем аддитивная мера (мера Хартли). Поясним это на следующем примере. Если мы подбрасываем монету, то получим сообщение из двух возможных состояний (орел или решка), то есть, алфавит сообщений из двух букв. Если подбрасываем кубик, одна грань которого голубая, а остальные грани окрашены в розовый цвет, то здесь также имеем алфавит из двух букв (голубой или розовый). Чтобы записать полученный текст (сообщение), в обоих случаях достаточно одной двоичной цифры на букву (п=1, т=2).
По Хартли здесь в обоих случаях
I= n
.
Но мы знаем, что в первом случае вероятность каждого исхода опыта равна 0,5 (
=0,5). А во втором случае 
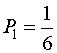и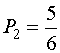 
соответственно. Мера Хартли не учитывает этого.
При равновероятности символов (частный случай) формула Шеннона вырождается в формулу Хартли:
I= -n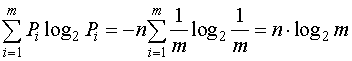
.
Для случая с монетой:
I= -1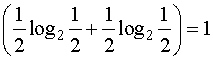
.
Для случая с кубиком:
I= -1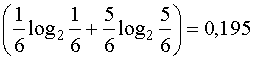
.
Количество информации, приходящейся на один элемент сообщения, называется удельной информативностью или энтропией.
Н=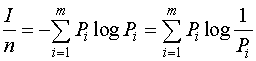 
. (1.6)
Количество информации и энтропия являются логарифмическими мерами и измеряются в одних и тех же единицах. Основание логарифма определяет единицу измерения количества информации и энтропии. Двоичная единица соответствует основанию логарифма, равному двум, и называется битом. Один бит - это количество информации в сообщении в одном из двух равновероятностных исходов некоторого опыта. Используются также натуральные (НИТ) и десятичные (ДИТ) логарифмы. Аналогичными единицами пользуются и при оценке количества информации с помощью меры Хартли.
Из формулы Шеннона следует, что количество информации, содержащейся в сообщении, зависит от числа элементов сообщения п, алфавита т и вероятностей выбора элементов 
. Зависимость I от п является линейной.
Отметим некоторые свойства энтропии.
1. Энтропия является величиной вещественной, ограниченной и неотрицательной, то есть Н>0. Это свойство следует из выражения (1.6).
2. Энтропия минимальна и равна нулю, если сообщение известно заранее, то есть если 
=1, а
.
3. Энтропия максимальна, если все состояния элементов сообщений равновероятны.
Н=
, если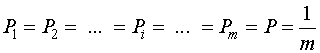 
. (1.7)
Величину максимальной энтропии найдем при использовании (1.6) и (1.7):
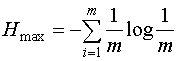=logm .
4. Энтропия бинарных (двоичных) сообщений может изменяться от нуля до единицы (двоичный алфавит, следовательно, т=2.)
Н=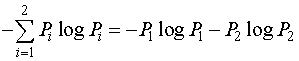
.
Используя условие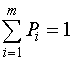 
и обозначив 
=Р, получим 
, а энтропия определится выражением
Н= -P logP - (1 - P)log(1 - P) .
Энтропия достигает максимума, равного единице, при 
= 
=0,5.
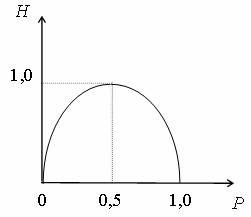
Рис. 1.3 - График функции Н= -Р logP - (1 - P)log(1 - P)
Семантические меры информации
Семантические меры информации оценивают смысл, содержание информации, ее целесообразность и существенность.
Целесообразность, полезность информации для решения какой-то задачи можно оценить по эффекту, который оказывает полученная информация на решение задачи. Если вероятность достижения цели увеличивается, то информацию следует считать полезной.
